pixyz.losses (Loss API)¶
Loss¶
-
class
pixyz.losses.losses.Loss(input_var=None)[source]¶ Bases:
torch.nn.modules.module.ModuleLoss class. In Pixyz, all loss classes are required to inherit this class.
Examples
>>> import torch >>> from torch.nn import functional as F >>> from pixyz.distributions import Bernoulli, Normal >>> from pixyz.losses import KullbackLeibler ... >>> # Set distributions >>> class Inference(Normal): ... def __init__(self): ... super().__init__(var=["z"],cond_var=["x"],name="q") ... self.model_loc = torch.nn.Linear(128, 64) ... self.model_scale = torch.nn.Linear(128, 64) ... def forward(self, x): ... return {"loc": self.model_loc(x), "scale": F.softplus(self.model_scale(x))} ... >>> class Generator(Bernoulli): ... def __init__(self): ... super().__init__(var=["x"],cond_var=["z"],name="p") ... self.model = torch.nn.Linear(64, 128) ... def forward(self, z): ... return {"probs": torch.sigmoid(self.model(z))} ... >>> p = Generator() >>> q = Inference() >>> prior = Normal(loc=torch.tensor(0.), scale=torch.tensor(1.), ... var=["z"], features_shape=[64], name="p_{prior}") ... >>> # Define a loss function (VAE) >>> reconst = -p.log_prob().expectation(q) >>> kl = KullbackLeibler(q,prior) >>> loss_cls = (reconst - kl).mean() >>> print(loss_cls) mean \left(- D_{KL} \left[q(z|x)||p_{prior}(z) \right] - \mathbb{E}_{q(z|x)} \left[\log p(x|z) \right] \right) >>> # Evaluate this loss function >>> data = torch.randn(1, 128) # Pseudo data >>> loss = loss_cls.eval({"x": data}) >>> print(loss) # doctest: +SKIP tensor(65.5939, grad_fn=<MeanBackward0>)
-
__init__(input_var=None)[source]¶ Parameters: input_var ( listofstr, defaults to None) – Input variables of this loss function. In general, users do not need to set them explicitly because these depend on the given distributions and each loss function.
-
input_var¶ Input variables of this distribution.
Type: list
-
loss_text¶
-
abs()[source]¶ Return an instance of
pixyz.losses.losses.AbsLoss.Returns: An instance of pixyz.losses.losses.AbsLossReturn type: pixyz.losses.losses.AbsLoss
-
mean()[source]¶ Return an instance of
pixyz.losses.losses.BatchMean.Returns: An instance of pixyz.losses.BatchMeanReturn type: pixyz.losses.losses.BatchMean
-
sum()[source]¶ Return an instance of
pixyz.losses.losses.BatchSum.Returns: An instance of pixyz.losses.losses.BatchSumReturn type: pixyz.losses.losses.BatchSum
-
detach()[source]¶ Return an instance of
pixyz.losses.losses.Detach.Returns: An instance of pixyz.losses.losses.DetachReturn type: pixyz.losses.losses.Detach
-
expectation(p, sample_shape=torch.Size([]))[source]¶ Return an instance of
pixyz.losses.Expectation.Parameters: - p (pixyz.distributions.Distribution) – Distribution for sampling.
- sample_shape (
listorNoneType, defaults to torch.Size()) – Shape of generating samples.
Returns: An instance of
pixyz.losses.ExpectationReturn type:
-
constant_var(constant_dict)[source]¶ Return an instance of
pixyz.losses.ConstantVar.Parameters: constant_dict (dict) – constant variables. Returns: An instance of pixyz.losses.ConstantVarReturn type: pixyz.losses.ConstantVar
-
eval(x_dict={}, return_dict=False, return_all=True, **kwargs)[source]¶ Evaluate the value of the loss function given inputs (
x_dict).Parameters: - x_dict (
dict, defaults to {}) – Input variables. - return_dict (bool, default to False.) – Whether to return samples along with the evaluated value of the loss function.
- return_all (bool, default to True.) – Whether to return all samples, including those that have not been updated.
Returns: - loss (torch.Tensor) – the evaluated value of the loss function.
- x_dict (
dict) – All samples generated when evaluating the loss function. Ifreturn_dictis False, it is not returned.
- x_dict (
-
Probability density function¶
LogProb¶
-
class
pixyz.losses.LogProb(p, sum_features=True, feature_dims=None)[source]¶ Bases:
pixyz.losses.losses.LossThe log probability density/mass function.
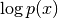
Examples
>>> import torch >>> from pixyz.distributions import Normal >>> p = Normal(loc=torch.tensor(0.), scale=torch.tensor(1.), var=["x"], ... features_shape=[10]) >>> loss_cls = LogProb(p) # or p.log_prob() >>> print(loss_cls) \log p(x) >>> sample_x = torch.randn(2, 10) # Psuedo data >>> loss = loss_cls.eval({"x": sample_x}) >>> print(loss) # doctest: +SKIP tensor([12.9894, 15.5280])
Prob¶
-
class
pixyz.losses.Prob(p, sum_features=True, feature_dims=None)[source]¶ Bases:
pixyz.losses.pdf.LogProbThe probability density/mass function.
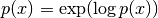
Examples
>>> import torch >>> from pixyz.distributions import Normal >>> p = Normal(loc=torch.tensor(0.), scale=torch.tensor(1.), var=["x"], ... features_shape=[10]) >>> loss_cls = Prob(p) # or p.prob() >>> print(loss_cls) p(x) >>> sample_x = torch.randn(2, 10) # Psuedo data >>> loss = loss_cls.eval({"x": sample_x}) >>> print(loss) # doctest: +SKIP tensor([3.2903e-07, 5.5530e-07])
Expected value¶
Expectation¶
-
class
pixyz.losses.Expectation(p, f, sample_shape=torch.Size([1]), reparam=True)[source]¶ Bases:
pixyz.losses.losses.LossExpectation of a given function (Monte Carlo approximation).
![\mathbb{E}_{p(x)}[f(x)] \approx \frac{1}{L}\sum_{l=1}^L f(x_l),
\quad \text{where}\quad x_l \sim p(x).](_images/math/a0f0b15b062e557386df0ad3d279c43067936215.png)
Note that
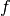 doesn’t need to be able to sample, which is known as the law of the unconscious statistician
(LOTUS).
doesn’t need to be able to sample, which is known as the law of the unconscious statistician
(LOTUS).Therefore, in this class,
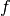 is assumed to
is assumed to pixyz.Loss.Examples
>>> import torch >>> from pixyz.distributions import Normal, Bernoulli >>> from pixyz.losses import LogProb >>> q = Normal(loc="x", scale=torch.tensor(1.), var=["z"], cond_var=["x"], ... features_shape=[10]) # q(z|x) >>> p = Normal(loc="z", scale=torch.tensor(1.), var=["x"], cond_var=["z"], ... features_shape=[10]) # p(x|z) >>> loss_cls = LogProb(p).expectation(q) # equals to Expectation(q, LogProb(p)) >>> print(loss_cls) \mathbb{E}_{p(z|x)} \left[\log p(x|z) \right] >>> sample_x = torch.randn(2, 10) # Psuedo data >>> loss = loss_cls.eval({"x": sample_x}) >>> print(loss) # doctest: +SKIP tensor([-12.8181, -12.6062]) >>> loss_cls = LogProb(p).expectation(q,sample_shape=(5,)) >>> loss = loss_cls.eval({"x": sample_x}) >>> print(loss) # doctest: +SKIP >>> q = Bernoulli(probs=torch.tensor(0.5), var=["x"], cond_var=[], features_shape=[10]) # q(x) >>> p = Bernoulli(probs=torch.tensor(0.3), var=["x"], cond_var=[], features_shape=[10]) # p(x) >>> loss_cls = p.log_prob().expectation(q,sample_shape=[64]) >>> train_loss = loss_cls.eval() >>> print(train_loss) # doctest: +SKIP tensor([46.7559]) >>> eval_loss = loss_cls.eval(test_mode=True) >>> print(eval_loss) # doctest: +SKIP tensor([-7.6047])
REINFORCE¶
-
pixyz.losses.REINFORCE(p, f, b=0, sample_shape=torch.Size([1]), reparam=True)[source]¶ Surrogate Loss for Policy Gradient Method (REINFORCE) with a given reward function
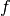 and a given baseline
and a given baseline 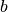 .
.![\mathbb{E}_{p(x)}[detach(f(x)-b(x))\log p(x)+f(x)-b(x)].](_images/math/ec6d646885eb67de48b1e6b5ffd0a7b643be4ffd.png)
in this function,
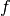 and
and 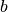 is assumed to
is assumed to pixyz.Loss.Parameters: - p (
pixyz.distributions.Distribution) – Distribution for expectation. - f (
pixyz.losses.Loss) – reward function - b (
pixyz.losses.Lossdefault to pixyz.losses.ValueLoss(0)) – baseline function - sample_shape (
torch.Sizedefault to torch.Size([1])) – sample size for expectation - reparam – using reparameterization in internal sampling
Returns: surrogate_loss – policy gradient can be calcurated from a gradient of this surrogate loss.
Return type: pixyz.losses.LossExamples
>>> import torch >>> from pixyz.distributions import Normal, Bernoulli >>> from pixyz.losses import LogProb >>> q = Bernoulli(probs=torch.tensor(0.5), var=["x"], cond_var=[], features_shape=[10]) # q(x) >>> p = Bernoulli(probs=torch.tensor(0.3), var=["x"], cond_var=[], features_shape=[10]) # p(x) >>> loss_cls = REINFORCE(q,p.log_prob(),sample_shape=[64]) >>> train_loss = loss_cls.eval(test_mode=True) >>> print(train_loss) # doctest: +SKIP tensor([46.7559]) >>> loss_cls = p.log_prob().expectation(q,sample_shape=[64]) >>> test_loss = loss_cls.eval() >>> print(test_loss) # doctest: +SKIP tensor([-7.6047])
- p (
Entropy¶
Entropy¶
-
pixyz.losses.Entropy(p, analytical=True, sample_shape=torch.Size([1]))[source]¶ Entropy (Analytical or Monte Carlo approximation).
![H(p) &= -\mathbb{E}_{p(x)}[\log p(x)] \qquad \text{(analytical)}\\
&\approx -\frac{1}{L}\sum_{l=1}^L \log p(x_l), \quad \text{where} \quad x_l \sim p(x) \quad \text{(MC approximation)}.](_images/math/cf1482b748a48232c0476307c352be0941f381b6.png)
Examples
>>> import torch >>> from pixyz.distributions import Normal >>> p = Normal(loc=torch.tensor(0.), scale=torch.tensor(1.), var=["x"], features_shape=[64]) >>> loss_cls = Entropy(p,analytical=True) >>> print(loss_cls) H \left[ {p(x)} \right] >>> loss_cls.eval() tensor([90.8121]) >>> loss_cls = Entropy(p,analytical=False,sample_shape=[10]) >>> print(loss_cls) - \mathbb{E}_{p(x)} \left[\log p(x) \right] >>> loss_cls.eval() # doctest: +SKIP tensor([90.5991])
CrossEntropy¶
-
pixyz.losses.CrossEntropy(p, q, analytical=False, sample_shape=torch.Size([1]))[source]¶ Cross entropy, a.k.a., the negative expected value of log-likelihood (Monte Carlo approximation or Analytical).
![H(p,q) &= -\mathbb{E}_{p(x)}[\log q(x)] \qquad \text{(analytical)}\\
&\approx -\frac{1}{L}\sum_{l=1}^L \log q(x_l), \quad \text{where} \quad x_l \sim p(x) \quad \text{(MC approximation)}.](_images/math/a1615f37c59dca7405ac9b92a95f8769072e6f7e.png)
Examples
>>> import torch >>> from pixyz.distributions import Normal >>> p = Normal(loc=torch.tensor(0.), scale=torch.tensor(1.), var=["x"], features_shape=[64], name="p") >>> q = Normal(loc=torch.tensor(1.), scale=torch.tensor(1.), var=["x"], features_shape=[64], name="q") >>> loss_cls = CrossEntropy(p,q,analytical=True) >>> print(loss_cls) D_{KL} \left[p(x)||q(x) \right] + H \left[ {p(x)} \right] >>> loss_cls.eval() tensor([122.8121]) >>> loss_cls = CrossEntropy(p,q,analytical=False,sample_shape=[10]) >>> print(loss_cls) - \mathbb{E}_{p(x)} \left[\log q(x) \right] >>> loss_cls.eval() # doctest: +SKIP tensor([123.2192])
Lower bound¶
ELBO¶
-
pixyz.losses.ELBO(p, q, sample_shape=torch.Size([1]))[source]¶ The evidence lower bound (Monte Carlo approximation).
![\mathbb{E}_{q(z|x)}\left[\log \frac{p(x,z)}{q(z|x)}\right] \approx \frac{1}{L}\sum_{l=1}^L \log p(x, z_l),
\quad \text{where} \quad z_l \sim q(z|x).](_images/math/9b34edd5d26a61476f0b8e72e59e653399411f6c.png)
Note
This class is a special case of the
Expectationclass.Examples
>>> import torch >>> from pixyz.distributions import Normal >>> q = Normal(loc="x", scale=torch.tensor(1.), var=["z"], cond_var=["x"], features_shape=[64]) # q(z|x) >>> p = Normal(loc="z", scale=torch.tensor(1.), var=["x"], cond_var=["z"], features_shape=[64]) # p(x|z) >>> loss_cls = ELBO(p,q) >>> print(loss_cls) \mathbb{E}_{p(z|x)} \left[\log p(x|z) - \log p(z|x) \right] >>> loss = loss_cls.eval({"x": torch.randn(1, 64)})
Statistical distance¶
KullbackLeibler¶
-
pixyz.losses.KullbackLeibler(p, q, dim=None, analytical=True, sample_shape=torch.Size([1]))[source]¶ Kullback-Leibler divergence (analytical or Monte Carlo Apploximation).
![D_{KL}[p||q] &= \mathbb{E}_{p(x)}\left[\log \frac{p(x)}{q(x)}\right] \qquad \text{(analytical)}\\
&\approx \frac{1}{L}\sum_{l=1}^L \log\frac{p(x_l)}{q(x_l)},
\quad \text{where} \quad x_l \sim p(x) \quad \text{(MC approximation)}.](_images/math/199f394c2d8d523f80de39e58f3bfd1fef0ad931.png)
Examples
>>> import torch >>> from pixyz.distributions import Normal, Beta >>> p = Normal(loc=torch.tensor(0.), scale=torch.tensor(1.), var=["z"], features_shape=[64], name="p") >>> q = Normal(loc=torch.tensor(1.), scale=torch.tensor(1.), var=["z"], features_shape=[64], name="q") >>> loss_cls = KullbackLeibler(p,q,analytical=True) >>> print(loss_cls) D_{KL} \left[p(z)||q(z) \right] >>> loss_cls.eval() tensor([32.]) >>> loss_cls = KullbackLeibler(p,q,analytical=False,sample_shape=[64]) >>> print(loss_cls) \mathbb{E}_{p(z)} \left[\log p(z) - \log q(z) \right] >>> loss_cls.eval() # doctest: +SKIP tensor([31.4713])
WassersteinDistance¶
-
class
pixyz.losses.WassersteinDistance(p, q, metric=PairwiseDistance())[source]¶ Bases:
pixyz.losses.losses.DivergenceWasserstein distance.
![W(p, q) = \inf_{\Gamma \in \mathcal{P}(x_p\sim p, x_q\sim q)} \mathbb{E}_{(x_p, x_q) \sim \Gamma}[d(x_p, x_q)]](_images/math/ffe52a4f83e762b329ce01c9e40a3970fdea6de7.png)
However, instead of the above true distance, this class computes the following one.
![W'(p, q) = \mathbb{E}_{x_p\sim p, x_q \sim q}[d(x_p, x_q)].](_images/math/114d1c08cc49f55c03d3f6e02f3d1b99839c0c40.png)
Here,
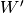 is the upper of
is the upper of 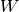 (i.e.,
(i.e., 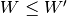 ), and these are equal when both
), and these are equal when both 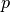 and
and 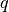 are degenerate (deterministic) distributions.
are degenerate (deterministic) distributions.Examples
>>> import torch >>> from pixyz.distributions import Normal >>> p = Normal(loc="x", scale=torch.tensor(1.), var=["z"], cond_var=["x"], features_shape=[64], name="p") >>> q = Normal(loc="x", scale=torch.tensor(1.), var=["z"], cond_var=["x"], features_shape=[64], name="q") >>> loss_cls = WassersteinDistance(p, q) >>> print(loss_cls) W^{upper} \left(p(z|x), q(z|x) \right) >>> loss = loss_cls.eval({"x": torch.randn(1, 64)})
MMD¶
-
class
pixyz.losses.MMD(p, q, kernel='gaussian', **kernel_params)[source]¶ Bases:
pixyz.losses.losses.DivergenceThe Maximum Mean Discrepancy (MMD).
![D_{MMD^2}[p||q] = \mathbb{E}_{p(x), p(x')}[k(x, x')] + \mathbb{E}_{q(x), q(x')}[k(x, x')]
- 2\mathbb{E}_{p(x), q(x')}[k(x, x')]](_images/math/4d6ab2e5bede99f83af1b9495221f4e554a39e29.png)
where
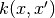 is any positive definite kernel.
is any positive definite kernel.Examples
>>> import torch >>> from pixyz.distributions import Normal >>> p = Normal(loc="x", scale=torch.tensor(1.), var=["z"], cond_var=["x"], features_shape=[64], name="p") >>> q = Normal(loc="x", scale=torch.tensor(1.), var=["z"], cond_var=["x"], features_shape=[64], name="q") >>> loss_cls = MMD(p, q, kernel="gaussian") >>> print(loss_cls) D_{MMD^2} \left[p(z|x)||q(z|x) \right] >>> loss = loss_cls.eval({"x": torch.randn(1, 64)}) >>> # Use the inverse (multi-)quadric kernel >>> loss = MMD(p, q, kernel="inv-multiquadratic").eval({"x": torch.randn(10, 64)})
Adversarial statistical distance¶
AdversarialJensenShannon¶
-
class
pixyz.losses.AdversarialJensenShannon(p, q, discriminator, optimizer=<class 'torch.optim.adam.Adam'>, optimizer_params={}, inverse_g_loss=True)[source]¶ Bases:
pixyz.losses.adversarial_loss.AdversarialLossJensen-Shannon divergence (adversarial training).
![D_{JS}[p(x)||q(x)] \leq 2 \cdot D_{JS}[p(x)||q(x)] + 2 \log 2
= \mathbb{E}_{p(x)}[\log d^*(x)] + \mathbb{E}_{q(x)}[\log (1-d^*(x))],](_images/math/39deab6cf70e24d0d737baa91aff3d971db218b0.png)
where
![d^*(x) = \arg\max_{d} \mathbb{E}_{p(x)}[\log d(x)] + \mathbb{E}_{q(x)}[\log (1-d(x))]](_images/math/08bd6dc585dcdcb77beb4ac7120aba79a8e85298.png) .
.This class acts as a metric that evaluates a given distribution (generator). If you want to learn this evaluation metric itself, i.e., discriminator (critic), use the
trainmethod.Examples
>>> import torch >>> from pixyz.distributions import Deterministic, EmpiricalDistribution, Normal >>> # Generator >>> class Generator(Deterministic): ... def __init__(self): ... super(Generator, self).__init__(var=["x"], cond_var=["z"], name="p") ... self.model = nn.Linear(32, 64) ... def forward(self, z): ... return {"x": self.model(z)} >>> p_g = Generator() >>> prior = Normal(loc=torch.tensor(0.), scale=torch.tensor(1.), ... var=["z"], features_shape=[32], name="p_{prior}") >>> p = (p_g*prior).marginalize_var("z") >>> print(p) Distribution: p(x) = \int p(x|z)p_{prior}(z)dz Network architecture: p_{prior}(z): Normal( name=p_{prior}, distribution_name=Normal, var=['z'], cond_var=[], input_var=[], features_shape=torch.Size([32]) (loc): torch.Size([1, 32]) (scale): torch.Size([1, 32]) ) p(x|z): Generator( name=p, distribution_name=Deterministic, var=['x'], cond_var=['z'], input_var=['z'], features_shape=torch.Size([]) (model): Linear(in_features=32, out_features=64, bias=True) ) >>> # Data distribution (dummy distribution) >>> p_data = EmpiricalDistribution(["x"]) >>> print(p_data) Distribution: p_{data}(x) Network architecture: EmpiricalDistribution( name=p_{data}, distribution_name=Data distribution, var=['x'], cond_var=[], input_var=['x'], features_shape=torch.Size([]) ) >>> # Discriminator (critic) >>> class Discriminator(Deterministic): ... def __init__(self): ... super(Discriminator, self).__init__(var=["t"], cond_var=["x"], name="d") ... self.model = nn.Linear(64, 1) ... def forward(self, x): ... return {"t": torch.sigmoid(self.model(x))} >>> d = Discriminator() >>> print(d) Distribution: d(t|x) Network architecture: Discriminator( name=d, distribution_name=Deterministic, var=['t'], cond_var=['x'], input_var=['x'], features_shape=torch.Size([]) (model): Linear(in_features=64, out_features=1, bias=True) ) >>> >>> # Set the loss class >>> loss_cls = AdversarialJensenShannon(p, p_data, discriminator=d) >>> print(loss_cls) mean(D_{JS}^{Adv} \left[p(x)||p_{data}(x) \right]) >>> >>> sample_x = torch.randn(2, 64) # Psuedo data >>> loss = loss_cls.eval({"x": sample_x}) >>> print(loss) # doctest: +SKIP tensor(1.3723, grad_fn=<AddBackward0>) >>> # For evaluating a discriminator loss, set the `discriminator` option to True. >>> loss_d = loss_cls.eval({"x": sample_x}, discriminator=True) >>> print(loss_d) # doctest: +SKIP tensor(1.4990, grad_fn=<AddBackward0>) >>> # When training the evaluation metric (discriminator), use the train method. >>> train_loss = loss_cls.loss_train({"x": sample_x})
References
[Goodfellow+ 2014] Generative Adversarial Networks
-
forward(x_dict, discriminator=False, **kwargs)[source]¶ Parameters: x_dict (dict) – Input variables. Returns: - a tuple of
pixyz.losses.Lossand dict - deterministically calcurated loss and updated all samples.
- a tuple of
-
d_loss(y_p, y_q, batch_n)[source]¶ Evaluate a discriminator loss given outputs of the discriminator.
Parameters: - y_p (torch.Tensor) – Output of discriminator given sample from p.
- y_q (torch.Tensor) – Output of discriminator given sample from q.
- batch_n (int) – Batch size of inputs.
Returns: Return type: torch.Tensor
-
g_loss(y_p, y_q, batch_n)[source]¶ Evaluate a generator loss given outputs of the discriminator.
Parameters: - y_p (torch.Tensor) – Output of discriminator given sample from p.
- y_q (torch.Tensor) – Output of discriminator given sample from q.
- batch_n (int) – Batch size of inputs.
Returns: Return type: torch.Tensor
-
AdversarialKullbackLeibler¶
-
class
pixyz.losses.AdversarialKullbackLeibler(p, q, discriminator, **kwargs)[source]¶ Bases:
pixyz.losses.adversarial_loss.AdversarialLossKullback-Leibler divergence (adversarial training).
![D_{KL}[p(x)||q(x)] = \mathbb{E}_{p(x)}\left[\log \frac{p(x)}{q(x)}\right]
\approx \mathbb{E}_{p(x)}\left[\log \frac{d^*(x)}{1-d^*(x)}\right],](_images/math/83f88fd933a50a1557bd3e6ff8192adce77a7ce8.png)
where
![d^*(x) = \arg\max_{d} \mathbb{E}_{q(x)}[\log d(x)] + \mathbb{E}_{p(x)}[\log (1-d(x))]](_images/math/c88b276c8780b91b02b8c9a9cdcaf8e9742297da.png) .
.Note that this divergence is minimized to close
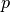 to
to 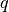 .
.Examples
>>> import torch >>> from pixyz.distributions import Deterministic, EmpiricalDistribution, Normal >>> # Generator >>> class Generator(Deterministic): ... def __init__(self): ... super(Generator, self).__init__(var=["x"], cond_var=["z"], name="p") ... self.model = nn.Linear(32, 64) ... def forward(self, z): ... return {"x": self.model(z)} >>> p_g = Generator() >>> prior = Normal(loc=torch.tensor(0.), scale=torch.tensor(1.), ... var=["z"], features_shape=[32], name="p_{prior}") >>> p = (p_g*prior).marginalize_var("z") >>> print(p) Distribution: p(x) = \int p(x|z)p_{prior}(z)dz Network architecture: p_{prior}(z): Normal( name=p_{prior}, distribution_name=Normal, var=['z'], cond_var=[], input_var=[], features_shape=torch.Size([32]) (loc): torch.Size([1, 32]) (scale): torch.Size([1, 32]) ) p(x|z): Generator( name=p, distribution_name=Deterministic, var=['x'], cond_var=['z'], input_var=['z'], features_shape=torch.Size([]) (model): Linear(in_features=32, out_features=64, bias=True) ) >>> # Data distribution (dummy distribution) >>> p_data = EmpiricalDistribution(["x"]) >>> print(p_data) Distribution: p_{data}(x) Network architecture: EmpiricalDistribution( name=p_{data}, distribution_name=Data distribution, var=['x'], cond_var=[], input_var=['x'], features_shape=torch.Size([]) ) >>> # Discriminator (critic) >>> class Discriminator(Deterministic): ... def __init__(self): ... super(Discriminator, self).__init__(var=["t"], cond_var=["x"], name="d") ... self.model = nn.Linear(64, 1) ... def forward(self, x): ... return {"t": torch.sigmoid(self.model(x))} >>> d = Discriminator() >>> print(d) Distribution: d(t|x) Network architecture: Discriminator( name=d, distribution_name=Deterministic, var=['t'], cond_var=['x'], input_var=['x'], features_shape=torch.Size([]) (model): Linear(in_features=64, out_features=1, bias=True) ) >>> >>> # Set the loss class >>> loss_cls = AdversarialKullbackLeibler(p, p_data, discriminator=d) >>> print(loss_cls) mean(D_{KL}^{Adv} \left[p(x)||p_{data}(x) \right]) >>> >>> sample_x = torch.randn(2, 64) # Psuedo data >>> loss = loss_cls.eval({"x": sample_x}) >>> # The evaluation value might be negative if the discriminator training is incomplete. >>> print(loss) # doctest: +SKIP tensor(-0.8377, grad_fn=<AddBackward0>) >>> # For evaluating a discriminator loss, set the `discriminator` option to True. >>> loss_d = loss_cls.eval({"x": sample_x}, discriminator=True) >>> print(loss_d) # doctest: +SKIP tensor(1.9321, grad_fn=<AddBackward0>) >>> # When training the evaluation metric (discriminator), use the train method. >>> train_loss = loss_cls.loss_train({"x": sample_x})
References
[Kim+ 2018] Disentangling by Factorising
-
forward(x_dict, discriminator=False, **kwargs)[source]¶ Parameters: x_dict (dict) – Input variables. Returns: - a tuple of
pixyz.losses.Lossand dict - deterministically calcurated loss and updated all samples.
- a tuple of
-
g_loss(y_p, batch_n)[source]¶ Evaluate a generator loss given an output of the discriminator.
Parameters: - y_p (torch.Tensor) – Output of discriminator given sample from p.
- batch_n (int) – Batch size of inputs.
Returns: Return type: torch.Tensor
-
d_loss(y_p, y_q, batch_n)[source]¶ Evaluate a discriminator loss given outputs of the discriminator.
Parameters: - y_p (torch.Tensor) – Output of discriminator given sample from p.
- y_q (torch.Tensor) – Output of discriminator given sample from q.
- batch_n (int) – Batch size of inputs.
Returns: Return type: torch.Tensor
-
AdversarialWassersteinDistance¶
-
class
pixyz.losses.AdversarialWassersteinDistance(p, q, discriminator, clip_value=0.01, **kwargs)[source]¶ Bases:
pixyz.losses.adversarial_loss.AdversarialJensenShannonWasserstein distance (adversarial training).
![W(p, q) = \sup_{||d||_{L} \leq 1} \mathbb{E}_{p(x)}[d(x)] - \mathbb{E}_{q(x)}[d(x)]](_images/math/76b508ff5d13d253e543ab112662841e28f09d32.png)
Examples
>>> import torch >>> from pixyz.distributions import Deterministic, EmpiricalDistribution, Normal >>> # Generator >>> class Generator(Deterministic): ... def __init__(self): ... super(Generator, self).__init__(var=["x"], cond_var=["z"], name="p") ... self.model = nn.Linear(32, 64) ... def forward(self, z): ... return {"x": self.model(z)} >>> p_g = Generator() >>> prior = Normal(loc=torch.tensor(0.), scale=torch.tensor(1.), ... var=["z"], features_shape=[32], name="p_{prior}") >>> p = (p_g*prior).marginalize_var("z") >>> print(p) Distribution: p(x) = \int p(x|z)p_{prior}(z)dz Network architecture: p_{prior}(z): Normal( name=p_{prior}, distribution_name=Normal, var=['z'], cond_var=[], input_var=[], features_shape=torch.Size([32]) (loc): torch.Size([1, 32]) (scale): torch.Size([1, 32]) ) p(x|z): Generator( name=p, distribution_name=Deterministic, var=['x'], cond_var=['z'], input_var=['z'], features_shape=torch.Size([]) (model): Linear(in_features=32, out_features=64, bias=True) ) >>> # Data distribution (dummy distribution) >>> p_data = EmpiricalDistribution(["x"]) >>> print(p_data) Distribution: p_{data}(x) Network architecture: EmpiricalDistribution( name=p_{data}, distribution_name=Data distribution, var=['x'], cond_var=[], input_var=['x'], features_shape=torch.Size([]) ) >>> # Discriminator (critic) >>> class Discriminator(Deterministic): ... def __init__(self): ... super(Discriminator, self).__init__(var=["t"], cond_var=["x"], name="d") ... self.model = nn.Linear(64, 1) ... def forward(self, x): ... return {"t": self.model(x)} >>> d = Discriminator() >>> print(d) Distribution: d(t|x) Network architecture: Discriminator( name=d, distribution_name=Deterministic, var=['t'], cond_var=['x'], input_var=['x'], features_shape=torch.Size([]) (model): Linear(in_features=64, out_features=1, bias=True) ) >>> >>> # Set the loss class >>> loss_cls = AdversarialWassersteinDistance(p, p_data, discriminator=d) >>> print(loss_cls) mean(W^{Adv} \left(p(x), p_{data}(x) \right)) >>> >>> sample_x = torch.randn(2, 64) # Psuedo data >>> loss = loss_cls.eval({"x": sample_x}) >>> print(loss) # doctest: +SKIP tensor(-0.0060, grad_fn=<SubBackward0>) >>> # For evaluating a discriminator loss, set the `discriminator` option to True. >>> loss_d = loss_cls.eval({"x": sample_x}, discriminator=True) >>> print(loss_d) # doctest: +SKIP tensor(-0.3802, grad_fn=<NegBackward>) >>> # When training the evaluation metric (discriminator), use the train method. >>> train_loss = loss_cls.loss_train({"x": sample_x})
References
[Arjovsky+ 2017] Wasserstein GAN
-
d_loss(y_p, y_q, *args, **kwargs)[source]¶ Evaluate a discriminator loss given outputs of the discriminator.
Parameters: - y_p (torch.Tensor) – Output of discriminator given sample from p.
- y_q (torch.Tensor) – Output of discriminator given sample from q.
- batch_n (int) – Batch size of inputs.
Returns: Return type: torch.Tensor
-
g_loss(y_p, y_q, *args, **kwargs)[source]¶ Evaluate a generator loss given outputs of the discriminator.
Parameters: - y_p (torch.Tensor) – Output of discriminator given sample from p.
- y_q (torch.Tensor) – Output of discriminator given sample from q.
- batch_n (int) – Batch size of inputs.
Returns: Return type: torch.Tensor
-
Loss for sequential distributions¶
IterativeLoss¶
-
class
pixyz.losses.IterativeLoss(step_loss, max_iter=None, series_var=(), update_value={}, slice_step=None, timestep_var=())[source]¶ Bases:
pixyz.losses.losses.LossIterative loss.
This class allows implementing an arbitrary model which requires iteration.
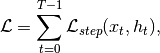
where
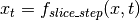 .
.Examples
>>> import torch >>> from torch.nn import functional as F >>> from pixyz.distributions import Normal, Bernoulli, Deterministic >>> >>> # Set distributions >>> x_dim = 128 >>> z_dim = 64 >>> h_dim = 32 >>> >>> # p(x|z,h_{prev}) >>> class Decoder(Bernoulli): ... def __init__(self): ... super().__init__(var=["x"],cond_var=["z", "h_prev"],name="p") ... self.fc = torch.nn.Linear(z_dim + h_dim, x_dim) ... def forward(self, z, h_prev): ... return {"probs": torch.sigmoid(self.fc(torch.cat((z, h_prev), dim=-1)))} ... >>> # q(z|x,h_{prev}) >>> class Encoder(Normal): ... def __init__(self): ... super().__init__(var=["z"],cond_var=["x", "h_prev"],name="q") ... self.fc_loc = torch.nn.Linear(x_dim + h_dim, z_dim) ... self.fc_scale = torch.nn.Linear(x_dim + h_dim, z_dim) ... def forward(self, x, h_prev): ... xh = torch.cat((x, h_prev), dim=-1) ... return {"loc": self.fc_loc(xh), "scale": F.softplus(self.fc_scale(xh))} ... >>> # f(h|x,z,h_{prev}) (update h) >>> class Recurrence(Deterministic): ... def __init__(self): ... super().__init__(var=["h"], cond_var=["x", "z", "h_prev"], name="f") ... self.rnncell = torch.nn.GRUCell(x_dim + z_dim, h_dim) ... def forward(self, x, z, h_prev): ... return {"h": self.rnncell(torch.cat((z, x), dim=-1), h_prev)} >>> >>> p = Decoder() >>> q = Encoder() >>> f = Recurrence() >>> >>> # Set the loss class >>> step_loss_cls = p.log_prob().expectation(q * f).mean() >>> print(step_loss_cls) mean \left(\mathbb{E}_{q(z,h|x,h_{prev})} \left[\log p(x|z,h_{prev}) \right] \right) >>> loss_cls = IterativeLoss(step_loss=step_loss_cls, ... series_var=["x"], update_value={"h": "h_prev"}) >>> print(loss_cls) \sum_{t=0}^{t_{max} - 1} mean \left(\mathbb{E}_{q(z,h|x,h_{prev})} \left[\log p(x|z,h_{prev}) \right] \right) >>> >>> # Evaluate >>> x_sample = torch.randn(30, 2, 128) # (timestep_size, batch_size, feature_size) >>> h_init = torch.zeros(2, 32) # (batch_size, h_dim) >>> loss = loss_cls.eval({"x": x_sample, "h_prev": h_init}) >>> print(loss) # doctest: +SKIP tensor(-2826.0906, grad_fn=<AddBackward0>
Loss for special purpose¶
Parameter¶
-
class
pixyz.losses.losses.Parameter(input_var)[source]¶ Bases:
pixyz.losses.losses.LossThis class defines a single variable as a loss class.
It can be used such as a coefficient parameter of a loss class.
Examples
>>> loss_cls = Parameter("x") >>> print(loss_cls) x >>> loss = loss_cls.eval({"x": 2}) >>> print(loss) 2
ValueLoss¶
-
class
pixyz.losses.losses.ValueLoss(loss1)[source]¶ Bases:
pixyz.losses.losses.LossThis class contains a scalar as a loss value.
If multiplying a scalar by an arbitrary loss class, this scalar is converted to the
ValueLoss.Examples
>>> loss_cls = ValueLoss(2) >>> print(loss_cls) 2 >>> loss = loss_cls.eval() >>> print(loss) tensor(2.)
ConstantVar¶
-
class
pixyz.losses.losses.ConstantVar(base_loss, constant_dict)[source]¶ Bases:
pixyz.losses.losses.LossThis class is defined as a loss class that makes the value of a variable a constant before evaluation.
It can be used to fix the coefficient parameters of the loss class or to condition random variables.
Examples
>>> loss_cls = Parameter('x').constant_var({'x': 1}) >>> print(loss_cls) x >>> loss = loss_cls.eval() >>> print(loss) 1
Operators¶
LossOperator¶
-
class
pixyz.losses.losses.LossOperator(loss1, loss2)[source]¶ Bases:
pixyz.losses.losses.Loss
LossSelfOperator¶
AddLoss¶
-
class
pixyz.losses.losses.AddLoss(loss1, loss2)[source]¶ Bases:
pixyz.losses.losses.LossOperatorApply the add operation to the two losses.
Examples
>>> loss_cls_1 = ValueLoss(2) >>> loss_cls_2 = Parameter("x") >>> loss_cls = loss_cls_1 + loss_cls_2 # equals to AddLoss(loss_cls_1, loss_cls_2) >>> print(loss_cls) x + 2 >>> loss = loss_cls.eval({"x": 3}) >>> print(loss) tensor(5.)
SubLoss¶
-
class
pixyz.losses.losses.SubLoss(loss1, loss2)[source]¶ Bases:
pixyz.losses.losses.LossOperatorApply the sub operation to the two losses.
Examples
>>> loss_cls_1 = ValueLoss(2) >>> loss_cls_2 = Parameter("x") >>> loss_cls = loss_cls_1 - loss_cls_2 # equals to SubLoss(loss_cls_1, loss_cls_2) >>> print(loss_cls) 2 - x >>> loss = loss_cls.eval({"x": 4}) >>> print(loss) tensor(-2.) >>> loss_cls = loss_cls_2 - loss_cls_1 # equals to SubLoss(loss_cls_2, loss_cls_1) >>> print(loss_cls) x - 2 >>> loss = loss_cls.eval({"x": 4}) >>> print(loss) tensor(2.)
MulLoss¶
-
class
pixyz.losses.losses.MulLoss(loss1, loss2)[source]¶ Bases:
pixyz.losses.losses.LossOperatorApply the mul operation to the two losses.
Examples
>>> loss_cls_1 = ValueLoss(2) >>> loss_cls_2 = Parameter("x") >>> loss_cls = loss_cls_1 * loss_cls_2 # equals to MulLoss(loss_cls_1, loss_cls_2) >>> print(loss_cls) 2 x >>> loss = loss_cls.eval({"x": 4}) >>> print(loss) tensor(8.)
DivLoss¶
-
class
pixyz.losses.losses.DivLoss(loss1, loss2)[source]¶ Bases:
pixyz.losses.losses.LossOperatorApply the div operation to the two losses.
Examples
>>> loss_cls_1 = ValueLoss(2) >>> loss_cls_2 = Parameter("x") >>> loss_cls = loss_cls_1 / loss_cls_2 # equals to DivLoss(loss_cls_1, loss_cls_2) >>> print(loss_cls) \frac{2}{x} >>> loss = loss_cls.eval({"x": 4}) >>> print(loss) tensor(0.5000) >>> loss_cls = loss_cls_2 / loss_cls_1 # equals to DivLoss(loss_cls_2, loss_cls_1) >>> print(loss_cls) \frac{x}{2} >>> loss = loss_cls.eval({"x": 4}) >>> print(loss) tensor(2.)
MinLoss¶
-
class
pixyz.losses.losses.MinLoss(loss1, loss2)[source]¶ Bases:
pixyz.losses.losses.LossOperatorApply the min operation to the loss.
Examples
>>> import torch >>> from pixyz.distributions import Normal >>> from pixyz.losses.losses import ValueLoss, Parameter, MinLoss >>> loss_min= MinLoss(ValueLoss(3), ValueLoss(1)) >>> print(loss_min) min \left(3, 1\right) >>> print(loss_min.eval()) tensor(1.)
MaxLoss¶
-
class
pixyz.losses.losses.MaxLoss(loss1, loss2)[source]¶ Bases:
pixyz.losses.losses.LossOperatorApply the max operation to the loss.
Examples
>>> import torch >>> from pixyz.distributions import Normal >>> from pixyz.losses.losses import ValueLoss, MaxLoss >>> loss_max= MaxLoss(ValueLoss(3), ValueLoss(1)) >>> print(loss_max) max \left(3, 1\right) >>> print(loss_max.eval()) tensor(3.)
NegLoss¶
-
class
pixyz.losses.losses.NegLoss(loss1)[source]¶ Bases:
pixyz.losses.losses.LossSelfOperatorApply the neg operation to the loss.
Examples
>>> loss_cls_1 = Parameter("x") >>> loss_cls = -loss_cls_1 # equals to NegLoss(loss_cls_1) >>> print(loss_cls) - x >>> loss = loss_cls.eval({"x": 4}) >>> print(loss) -4
AbsLoss¶
-
class
pixyz.losses.losses.AbsLoss(loss1)[source]¶ Bases:
pixyz.losses.losses.LossSelfOperatorApply the abs operation to the loss.
Examples
>>> import torch >>> from pixyz.distributions import Normal >>> from pixyz.losses import LogProb >>> p = Normal(loc=torch.tensor(0.), scale=torch.tensor(1.), var=["x"], ... features_shape=[10]) >>> loss_cls = LogProb(p).abs() # equals to AbsLoss(LogProb(p)) >>> print(loss_cls) |\log p(x)| >>> sample_x = torch.randn(2, 10) # Psuedo data >>> loss = loss_cls.eval({"x": sample_x}) >>> print(loss) # doctest: +SKIP tensor([12.9894, 15.5280])
BatchMean¶
-
class
pixyz.losses.losses.BatchMean(loss1)[source]¶ Bases:
pixyz.losses.losses.LossSelfOperatorAverage a loss class over given batch data.
![\mathbb{E}_{p_{data}(x)}[\mathcal{L}(x)] \approx \frac{1}{N}\sum_{i=1}^N \mathcal{L}(x_i),](_images/math/bf9d0a7488a0627d93f1206e1cac8c049f816a51.png)
where
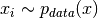 and
and 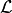 is a loss function.
is a loss function.Examples
>>> import torch >>> from pixyz.distributions import Normal >>> from pixyz.losses import LogProb >>> p = Normal(loc=torch.tensor(0.), scale=torch.tensor(1.), var=["x"], ... features_shape=[10]) >>> loss_cls = LogProb(p).mean() # equals to BatchMean(LogProb(p)) >>> print(loss_cls) mean \left(\log p(x) \right) >>> sample_x = torch.randn(2, 10) # Psuedo data >>> loss = loss_cls.eval({"x": sample_x}) >>> print(loss) # doctest: +SKIP tensor(-14.5038)
BatchSum¶
-
class
pixyz.losses.losses.BatchSum(loss1)[source]¶ Bases:
pixyz.losses.losses.LossSelfOperatorSummation a loss class over given batch data.
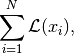
where
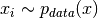 and
and 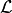 is a loss function.
is a loss function.Examples
>>> import torch >>> from pixyz.distributions import Normal >>> from pixyz.losses import LogProb >>> p = Normal(loc=torch.tensor(0.), scale=torch.tensor(1.), var=["x"], ... features_shape=[10]) >>> loss_cls = LogProb(p).sum() # equals to BatchSum(LogProb(p)) >>> print(loss_cls) sum \left(\log p(x) \right) >>> sample_x = torch.randn(2, 10) # Psuedo data >>> loss = loss_cls.eval({"x": sample_x}) >>> print(loss) # doctest: +SKIP tensor(-31.9434)
Detach¶
-
class
pixyz.losses.losses.Detach(loss1)[source]¶ Bases:
pixyz.losses.losses.LossSelfOperatorApply the detach method to the loss.
DataParalleledLoss¶
-
class
pixyz.losses.losses.DataParalleledLoss(loss, distributed=False, **kwargs)[source]¶ Bases:
pixyz.losses.losses.LossLoss class wrapper of torch.nn.DataParallel. It can be used as the original loss class. eval & forward methods support data-parallel running.
Examples
>>> import torch >>> from torch import optim >>> from torch.nn import functional as F >>> from pixyz.distributions import Bernoulli, Normal >>> from pixyz.losses import KullbackLeibler, DataParalleledLoss >>> from pixyz.models import Model >>> used_gpu_i = set() >>> used_gpu_g = set() >>> # Set distributions (Distribution API) >>> class Inference(Normal): ... def __init__(self): ... super().__init__(var=["z"],cond_var=["x"],name="q") ... self.model_loc = torch.nn.Linear(128, 64) ... self.model_scale = torch.nn.Linear(128, 64) ... def forward(self, x): ... used_gpu_i.add(x.device.index) ... return {"loc": self.model_loc(x), "scale": F.softplus(self.model_scale(x))} >>> class Generator(Bernoulli): ... def __init__(self): ... super().__init__(var=["x"],cond_var=["z"],name="p") ... self.model = torch.nn.Linear(64, 128) ... def forward(self, z): ... used_gpu_g.add(z.device.index) ... return {"probs": torch.sigmoid(self.model(z))} >>> p = Generator() >>> q = Inference() >>> prior = Normal(loc=torch.tensor(0.), scale=torch.tensor(1.), ... var=["z"], features_shape=[64], name="p_{prior}") >>> # Define a loss function (Loss API) >>> reconst = -p.log_prob().expectation(q) >>> kl = KullbackLeibler(q,prior) >>> batch_loss_cls = (reconst - kl) >>> # device settings >>> device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu") >>> device_count = torch.cuda.device_count() >>> if device_count > 1: ... loss_cls = DataParalleledLoss(batch_loss_cls).mean().to(device) ... else: ... loss_cls = batch_loss_cls.mean().to(device) >>> # Set a model (Model API) >>> model = Model(loss=loss_cls, distributions=[p, q], ... optimizer=optim.Adam, optimizer_params={"lr": 1e-3}) >>> # Train and test the model >>> data = torch.randn(2, 128).to(device) # Pseudo data >>> train_loss = model.train({"x": data}) >>> expected = set(range(device_count)) if torch.cuda.is_available() else {None} >>> assert used_gpu_i==expected >>> assert used_gpu_g==expected